Introduction:
Dynamic programming can be a game-changer when it comes to solving complex optimization problems. But did you know that there's a secret weapon within dynamic programming called memoization? In this blog post, we'll embark on a journey to demystify memoization and discover how it can supercharge your dynamic programming solutions. Get ready to level up your coding skills and harness the power of memoization!
What is Memoization, Anyway?
Why Memoization Matters in Dynamic Programming?
Memoization is like having a secret time-saving technique up your sleeve. In dynamic programming, problems often involve overlapping subproblems, which means you end up solving the same subproblems repeatedly. Without memoization, this can lead to inefficiencies and sluggish performance. But with memoization, you can store and reuse the results of expensive function calls, drastically reducing computation time.
Let's Get Memoizing: A Step-by-Step Guide Now that you understand the power of memoization, let's explore how to put it into action. Here's a beginner-friendly step-by-step guide to implementing memoization in your dynamic programming solutions:
Identify the Subproblems: Break down the problem into smaller, more manageable subproblems. Think of them as puzzle pieces that fit together to solve the big picture.
Create a Memoization Cache: Set up a special storage space, like a cool backpack or a digital memory bank, to store the results of solved subproblems. This cache will save you from doing repetitive work.
Check the Cache: Before diving into solving a subproblem, take a peek inside your cache. If you find the answer already there, celebrate and retrieve it! No need to go through the trouble of recalculating.
Compute and Store: If the answer is not in the cache, it's time to put your problem-solving skills to work. Solve the subproblem and store the result in the cache for future reference. You're building your library of answers!
Reap the Rewards: Return the result of the subproblem to where it was called from. Enjoy the speed, efficiency, and satisfaction of having optimized your dynamic programming solution with memoization.
For a Simple Example, let's say we are dealing with a Fibonacci series. The problem is asking you to find the nth Fibonacci number, given n is only a positive integer.
This is a sample solution in Python:


As you can observe, the initial recursive program took approximately 0.03 seconds in CPU time and 6.6 seconds in user time. However, we can significantly reduce the execution time to a fraction of a second by implementing a technique called memoization. This technique involves storing previously computed function results in a dictionary, where the input number serves as the key and the corresponding return value as the value. By doing so, we can eliminate redundant recursive function calls and retrieve precomputed values directly from the dictionary.
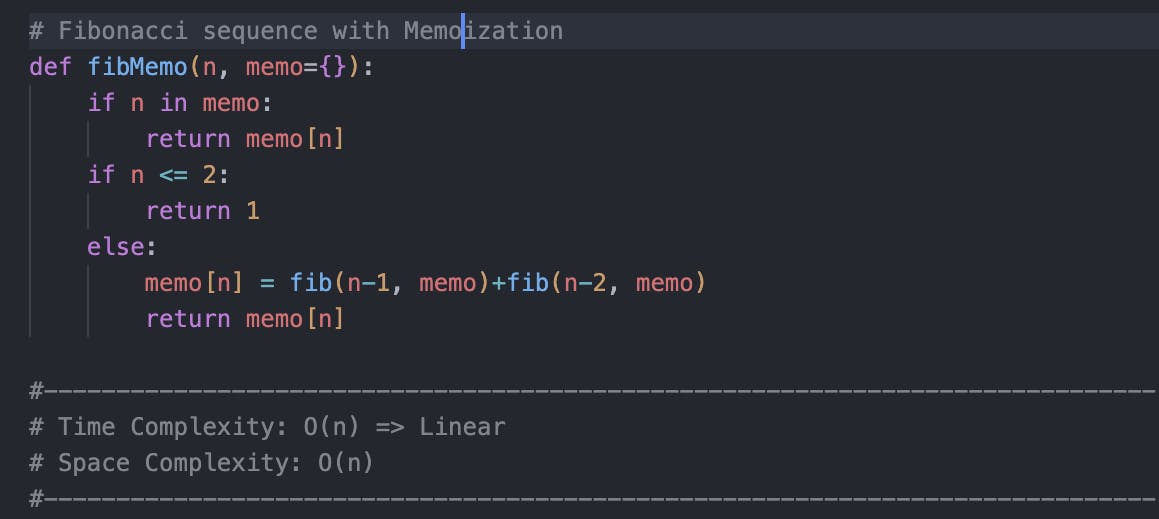

Now the runtime is drastically reduced and the exponential time complexity became linear.
Congratulations! You've unlocked the secret power of memoization in dynamic programming. By harnessing the magic of memoization, you can optimize your solutions, solve
